Chapitre 3 Mise en oeuvre pratique

3.1 Introduction

Dans ce chapitre, nous découvrirons deux outils très pratiques pour faire de la statistique bayésienne sans trop d’efforts : NIMBLE et brms. Il s’agit de deux packages R qui implémentent pour vous les algorithmes MCMC. Concrètement, il vous suffit de spécifier une vraisemblance et des priors pour que le théorème de Bayes s’applique automatiquement. Grâce à une syntaxe proche de celle de R, les deux packages rendent cette étape relativement simple, même pour des modèles complexes.

3.2 `NIMBLE`

NIMBLE signifie Numerical Inference for statistical Models using Bayesian and Likelihood Estimation. L’originalité de NIMBLE est qu’il distingue l’étape de la construction du modèle de l’étape d’ajustement du modèle à des données, ce qui permet une grande flexibilité dans la modélisation. Le package est développé par une équipe de scientifiques qui veille à améliorer les capacités du package selon les retours de la communauté. Cette communauté NIMBLE est active sur https://groups.google.com/g/nimble-users, un groupe dans lequel les développeurs du package répondent aux questions de manière bienveillante et rapide.

Pour utiliser NIMBLE, vous pouvez suivre les étapes suivantes :
1. Construire un modèle (vraisemblance et priors).
2. Lire les données.
3. Spécifier les paramètres sur lesquels on souhaite faire des inférences.
4. Fournir des valeurs initiales pour ces paramètres (par chaîne).
5. Définir les détails du MCMC : nombre de chaînes, burn-in, nombre d’itérations à la suite du burn-in.
6. Evaluer la convergence.
7. Interpréter les résultats.

Mais d’abord, ne pas oublier de charger le package (pour installer NIMBLE, voir https://r-nimble.org/download) :

library(nimble)

Reprenons notre exemple fil rouge sur la survie des ragondins. Première étape : définir la vraisemblance binomiale et un prior uniforme sur la probabilité de survie theta avec la fonction nimbleCode() :

model <- nimbleCode({
  # vraisemblance
  y ~ dbinom(theta, n)
  # prior
  theta ~ dbeta(1, 1) # ou dunif(0,1)
})

On peut vérifier que l’objet model contient bien ce code :

model
#> {
#>     y ~ dbinom(theta, n)
#>     theta ~ dbeta(1, 1)
#> }

Dans le code, y et n sont connus, seul theta est à estimer. La ligne y ~ dbinom(theta, n) indique que le nombre de survivants suit une loi binomiale. Le prior est une bêta de paramètres 1 et 1 (dbeta()), c’est-à-dire une uniforme entre 0 et 1 (dunif()). Les distributions classiques sont disponibles dans NIMBLE (dnorm, dpois, dmultinom, etc.). A noter que l’ordre des lignes n’a pas d’importance : NIMBLE utilise un langage déclaratif (vous dites quoi, pas comment).

Dans une deuxième étape, on entre les données dans une liste :

dat <- list(n = 57, y = 19)

NIMBLE distingue les données (valeurs connues à gauche de ~) des constantes (par ex. des indices de boucle). Déclarer certaines valeurs comme constantes peut améliorer l’efficacité du calcul, mais ce n’est pas toujours instinctif. Heureusement, NIMBLE s’en occupe en grande partie tout seul et vous proposera de déplacer certains objets en constantes si c’est plus efficace. Nous ignorerons cette distinction ici, mais on l’utilisera plus tard dans le Chapitre 6.

La troisième étape consiste à dire à NIMBLE quels sont les paramètres sur lesquels vous voulez faire des inférences. Ici, c’est la probabilité de survie theta qui nous intéresse :

par <- c("theta")

En général, votre modèle contient de nombreuses quantités, dont certaines sont peu intéressantes et ne valent pas la peine d’être suivies. Avoir un contrôle complet sur ce que l’on surveille est donc très utile.

La quatrième étape consiste à spécifier des valeurs initiales pour tous les paramètres du modèle. Au strict minimum, vous devez fournir des valeurs initiales pour toutes les quantités qui apparaissent uniquement à gauche du symbole ~ dans votre code, et qui ne sont pas fournies comme données.

Pour s’assurer que l’algorithme MCMC explore correctement la distribution a posteriori, on lance différentes chaînes avec des valeurs initiales différentes. Vous pouvez spécifier des valeurs initiales pour chaque chaîne (ici trois chaînes) dans une liste, que vous placez dans une autre liste :

init1 <- list(theta = 0.1) # chaîne 1
init2 <- list(theta = 0.5) # chaîne 2
init3 <- list(theta = 0.9) # chaîne 3
inits <- list(init1, init2, init3) # une liste de listes
inits
#> [[1]]
#> [[1]]$theta
#> [1] 0.1
#> 
#> 
#> [[2]]
#> [[2]]$theta
#> [1] 0.5
#> 
#> 
#> [[3]]
#> [[3]]$theta
#> [1] 0.9

Alternativement, vous pouvez écrire une fonction R qui génère des valeurs initiales aléatoires :

inits <- function() list(theta = runif(1,0,1))
inits()
#> $theta
#> [1] 0.6536282

Je préfère utiliser des fonctions car le code est plus compact et s’adapte automatiquement au nombre de chaînes. Si vous utilisez une fonction pour générer les valeurs initiales, il est toujours bon de fixer une graine aléatoire (‘seed’ en anglais) dans votre code avant de tirer les valeurs, vous pourrez ainsi en garder une trace. Par exemple :

graine <- 666
set.seed(graine)

Cinquième et dernière étape : vous devez indiquer à NIMBLE le nombre de chaînes à lancer (n.chains), la durée de la phase de burn-in (n.burnin), ainsi que le nombre total d’itérations (n.iter) à effectuer :

n.iter <- 2000
n.burnin <- 300
n.chains <- 3

Dans NIMBLE, vous spécifiez le nombre total d’itérations, donc le nombre d’échantillons postérieurs par chaîne sera égal à n.iter - n.burnin.

Au passage, pour déterminer de la longueur de la période de pré-chauffage ou burn-in, il suffit de faire tourner NIMBLE avec n.burnin <- 0 pour quelques centaines ou milliers d’itérations et d’examiner la trace du paramètre pour décider du nombre d’itérations à utiliser pour atteindre la convergence.

NIMBLE permet également de supprimer des échantillons après la phase de burn-in, ce qu’on appelle le thinning. Par défaut, thinning = 1 (aucun échantillon n’est retiré), ce qui signifie que toutes les simulations sont utilisées pour résumer les distributions a posteriori.

Nous avons maintenant tous les ingrédients pour exécuter notre modèle, c’est-à-dire pour générer des échantillons de la distribution a posteriori des paramètres via des simulations MCMC. On utilise pour cela la fonction nimbleMCMC() :

mcmc.output <- nimbleMCMC(code = model, # modèle
                          data = dat, # données
                          inits = inits, # valeurs initiales
                          monitors = par, # paramètres que l'on souhaite en sortie
                          niter = n.iter, # nombre total d'itérations
                          nburnin = n.burnin, # nombre d'itération du burn-in
                          nchains = n.chains) # nombre de chaînes
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|

NIMBLE effectue plusieurs étapes internes que nous ne détaillerons pas ici. La fonction nimbleMCMC() accepte d’autres arguments utiles. Par exemple, setSeed vous permet de fixer une graine aléatoire dans l’appel MCMC, ce qui garantit que vous obtenez exactement les mêmes chaînes à chaque exécution – très utile pour la reproductibilité et le débogage. Vous pouvez aussi obtenir un résumé des sorties avec summary = TRUE ou encore récupérer les échantillons MCMC au format coda::mcmc() avec samplesAsCodaMCMC = TRUE. Enfin vous pouvez supprimer la barre de progression avec progressBar = FALSE si vous trouvez cela trop déprimant pendant de longues simulations. Consultez ?nimbleMCMC pour plus de détails.

Jetons un coup d’oeil aux résultats, en commençant par examiner ce que contient l’objet mcmc.output :

str(mcmc.output)
#> List of 3
#>  $ chain1: num [1:1700, 1] 0.401 0.367 0.376 0.279 0.363 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr "theta"
#>  $ chain2: num [1:1700, 1] 0.351 0.31 0.319 0.329 0.354 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr "theta"
#>  $ chain3: num [1:1700, 1] 0.322 0.215 0.338 0.352 0.438 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr "theta"

L’objet R mcmc.output est une liste composée de trois éléments, un pour chaque chaîne MCMC. Jetons un oeil par exemple à la première chaîne :

dim(mcmc.output$chain1)
#> [1] 1700    1
head(mcmc.output$chain1)
#>          theta
#> [1,] 0.4005633
#> [2,] 0.3671535
#> [3,] 0.3758171
#> [4,] 0.2789161
#> [5,] 0.3630945
#> [6,] 0.2989659

Chaque composant de la liste est une matrice. Les lignes correspondent aux 1700 échantillons issus de la distribution a posteriori de $\theta$ (ce qui correspond à n.iter - n.burnin itérations). Les colonnes représentent les paramètres que nous surveillons, ici theta.

À partir de là, on peut calculer la moyenne a posteriori de $\theta$ :

mean(mcmc.output$chain1[,"theta"])
#> [1] 0.3400862

Et l’intervalle de crédibilité à 95 % :

quantile(mcmc.output$chain1[,"theta"], probs = c(2.5, 97.5)/100)
#>      2.5%     97.5% 
#> 0.2276521 0.4663676

Visualisons maintenant la distribution a posteriori de $\theta$ sous forme d’un histogramme (Figure 3.1) :

mcmc.output$chain1[,"theta"] %>%
  as_tibble() %>%
  ggplot() +
  geom_histogram(aes(x = value), color = "white") +
  labs(x = "Probabilité de survie")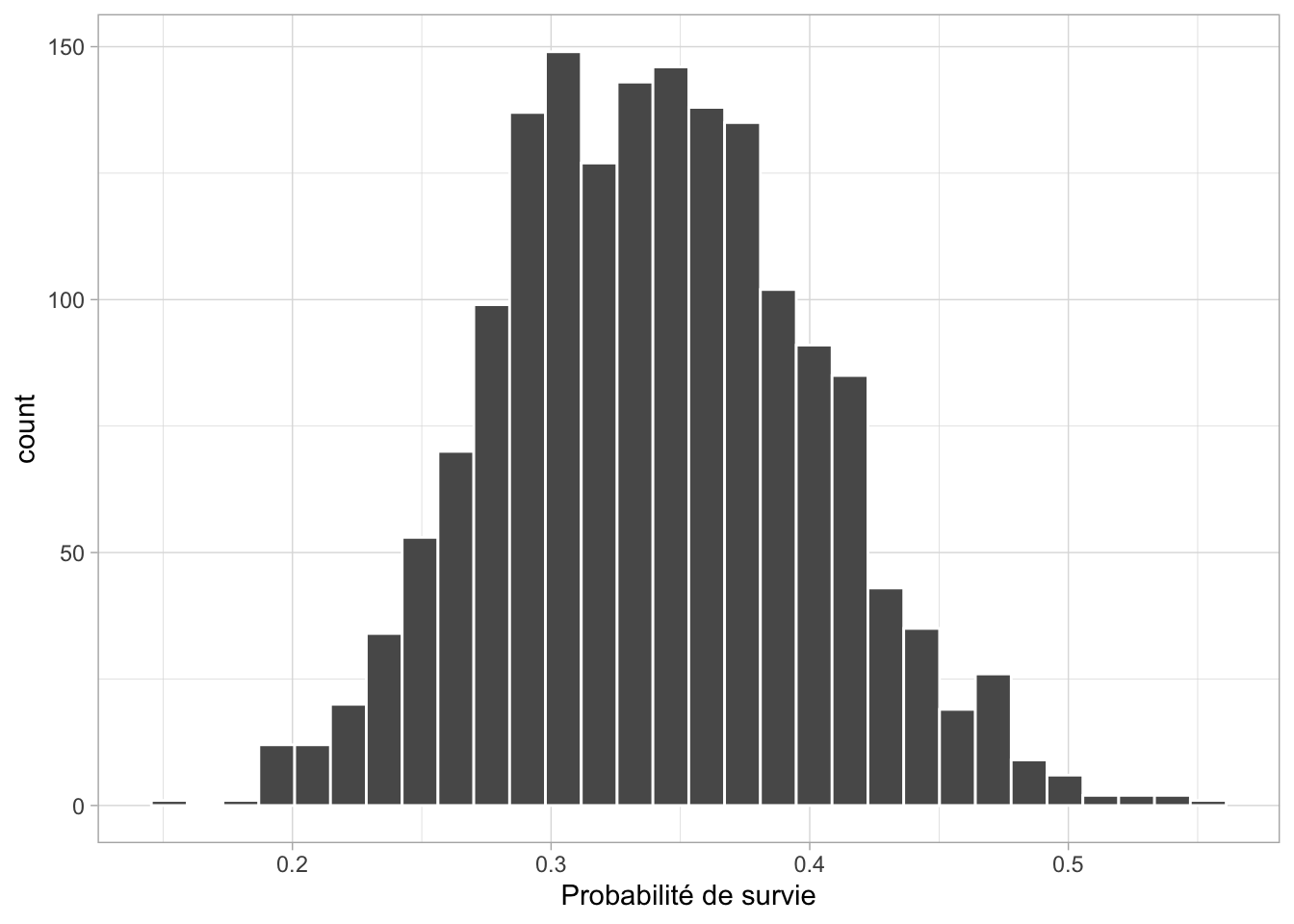

$Histogramme de la distribution a posteriori de la probabilité de survie ($\theta$)$

Figure 3.1: Histogramme de la distribution a posteriori de la probabilité de survie ($\theta$)

Il existe des façons plus pratiques de faire ces inférences bayésiennes. Nous utiliserons le package R MCMCvis pour résumer et visualiser les sorties MCMC, mais vous pouvez aussi utiliser ggmcmc, bayesplot, ou encore basicMCMCplots.

Chargeons MCMCvis :

library(MCMCvis)

Pour obtenir les résumés numériques les plus courants, on utilise MCMCsummary() :

MCMCsummary(object = mcmc.output, round = 2)
#>       mean   sd 2.5%  50% 97.5% Rhat n.eff
#> theta 0.34 0.06 0.23 0.34  0.46    1  4865

On peut également tracer un “caterpillar plot” avec MCMCplot() pour visualiser les distributions a posteriori (Figure 3.2) :

MCMCplot(object = mcmc.output, params = 'theta')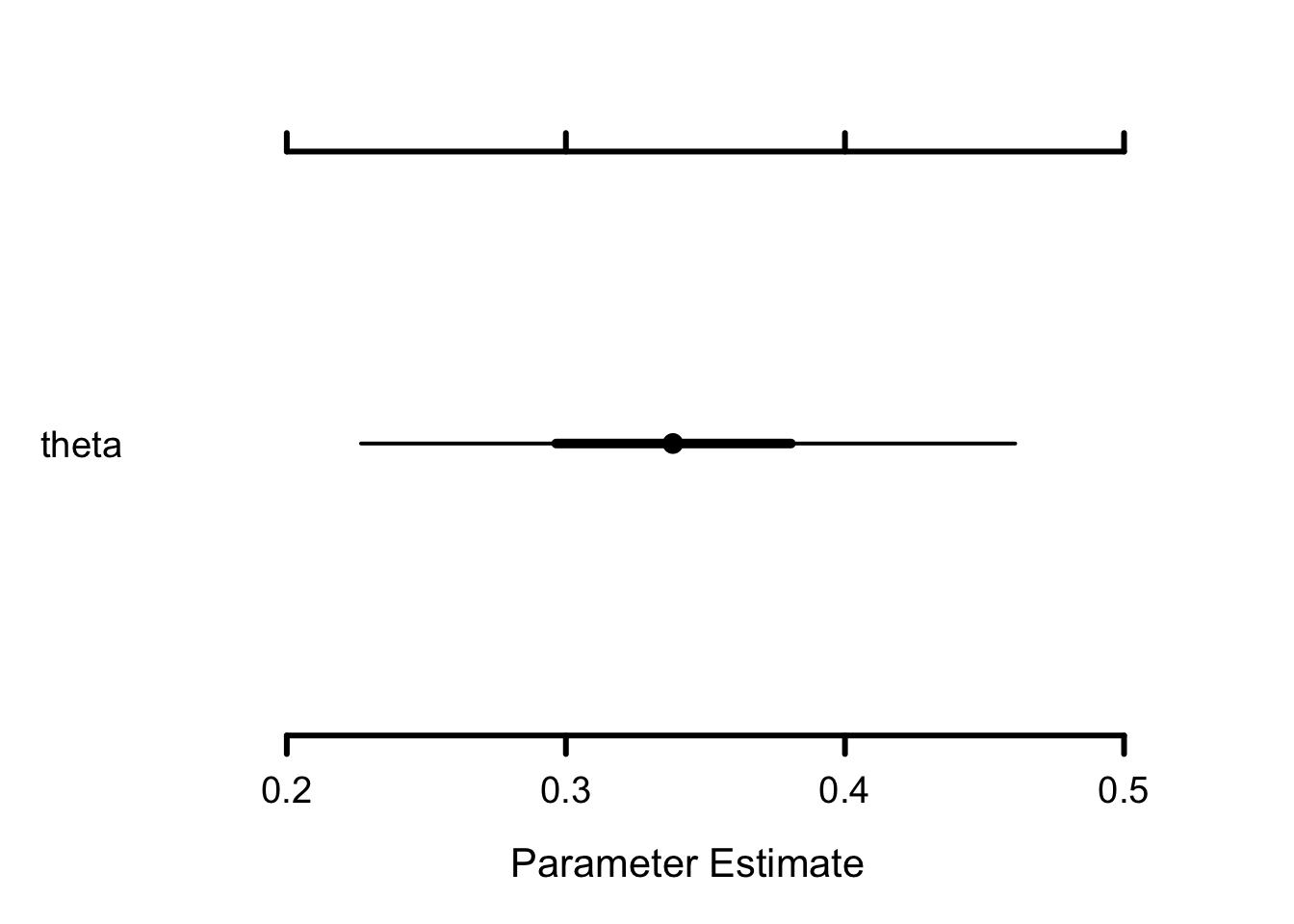

$Caterpillar plot de la distribution a posteriori de la probabilité de survie ($\theta$)$

Figure 3.2: Caterpillar plot de la distribution a posteriori de la probabilité de survie ($\theta$)

Le point représente la médiane a posteriori, la barre épaisse l’intervalle de crédibilité à 50 % et la fine l’intervalle à 95 %.

On peut tracer la chaîne MCMC (trace plot) et la densité a posteriori associée avec MCMCtrace() (Figure 3.3) :

MCMCtrace(object = mcmc.output,
          pdf = FALSE, # ne pas exporter en PDF
          ind = TRUE,  # une courbe par chaîne
          params = "theta")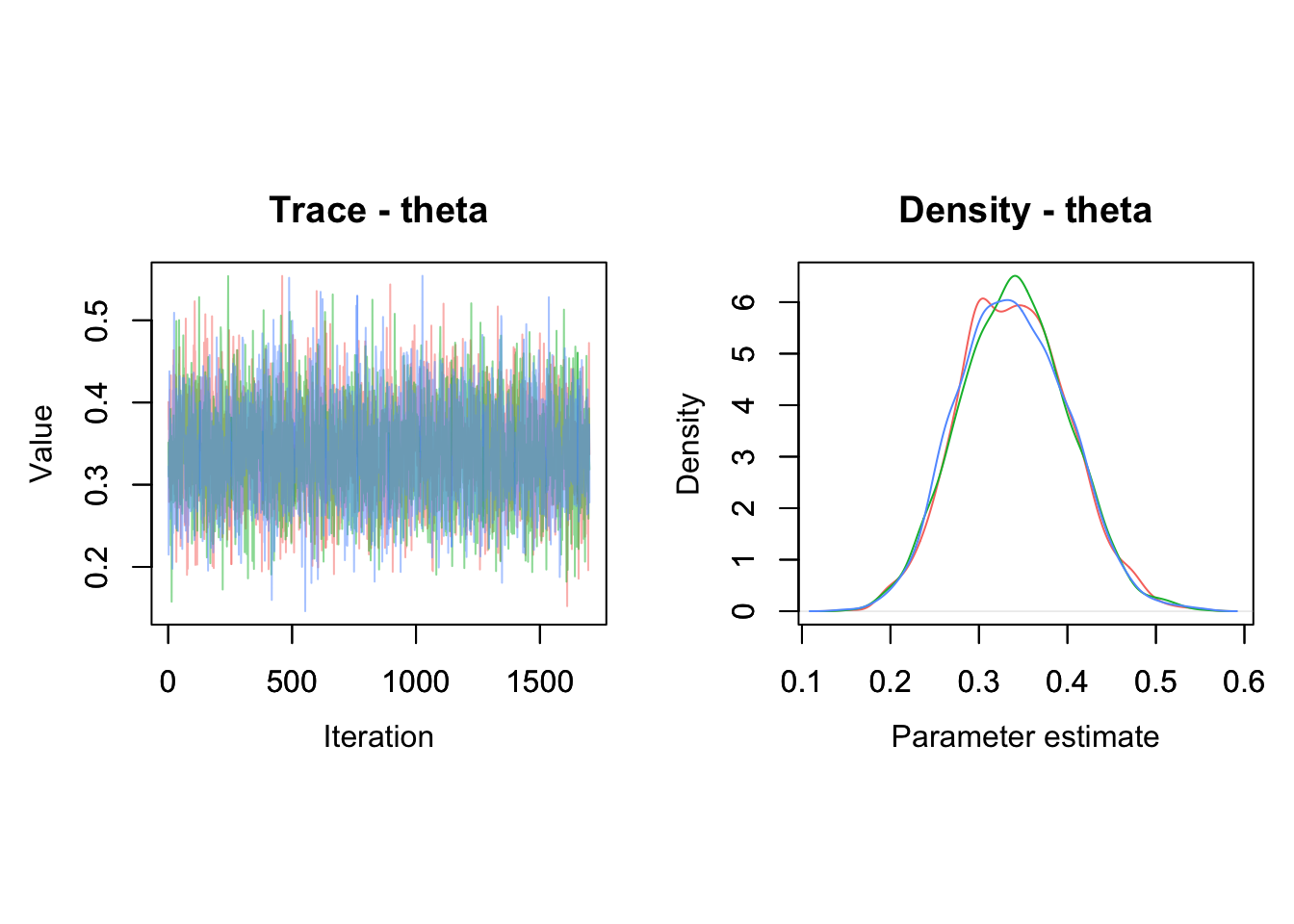

$Trace plot et densité a posteriori de la probabilité de survie ($\theta$)$

Figure 3.3: Trace plot et densité a posteriori de la probabilité de survie ($\theta$)

Ces représentations servent à évaluer la convergence des chaînes et à détecter d’éventuels problèmes d’estimation (voir le Chapitre 2). On peut aussi ajouter les diagnostics vus précédemment (Figure 3.4) ; la taille d’échantillon efficace est 5100 et correspond à 3 chaînes dont on conserve les 2000 - 300 valeurs simulées après burn-in :

MCMCtrace(object = mcmc.output,
          pdf = FALSE,
          ind = TRUE,
          Rhat = TRUE, # ajoute le Rhat
          n.eff = TRUE, # ajoute la taille d’échantillon effective
          params = "theta")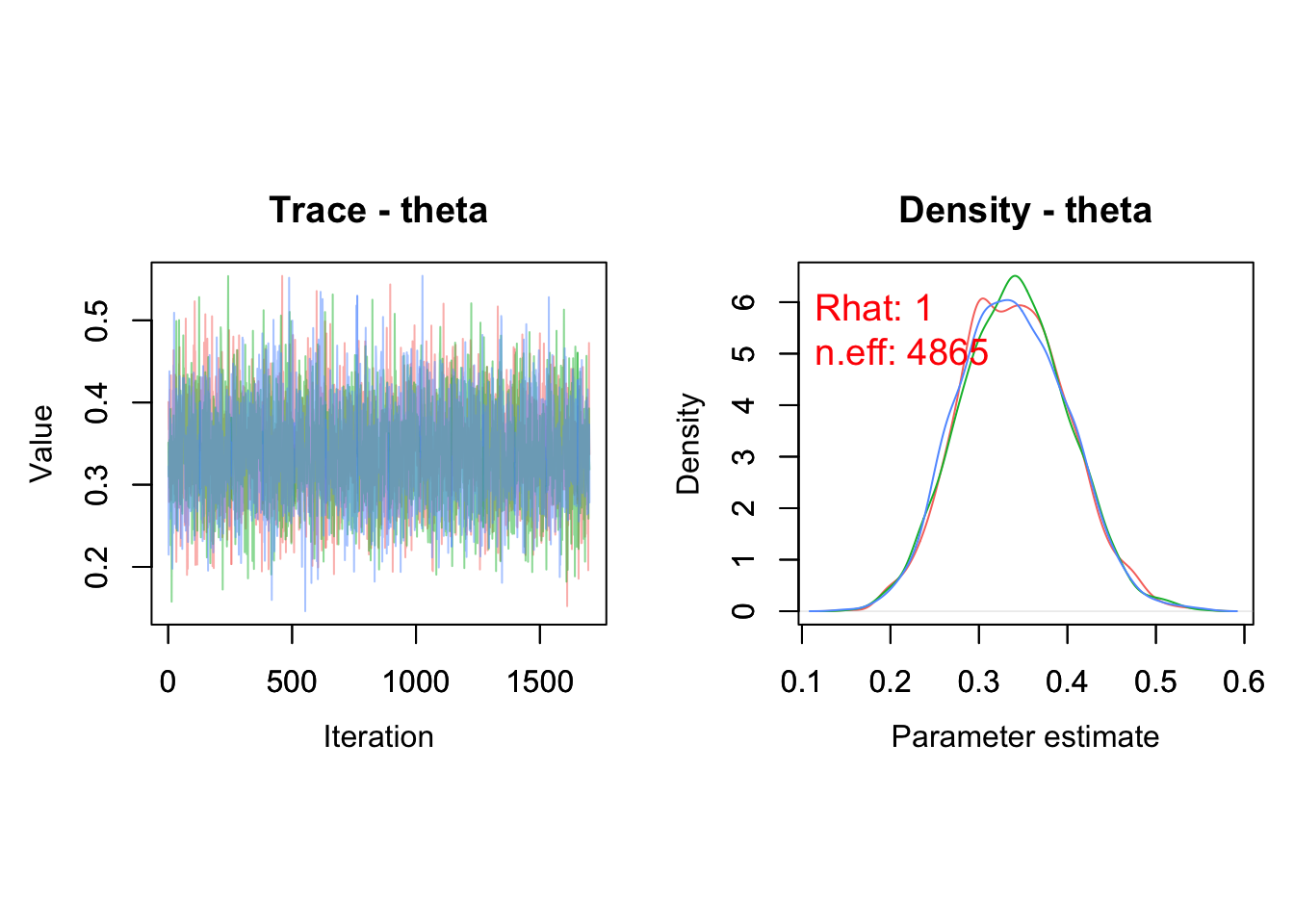

$Trace plot et densité a posteriori de la probabilité de survie ($\theta$) avec les diagnostics de convergence.$

Figure 3.4: Trace plot et densité a posteriori de la probabilité de survie ($\theta$) avec les diagnostics de convergence.

Dans notre exemple, il suffit de rassembler les échantillons de theta issus des trois chaînes :

theta_samples <- c(mcmc.output$chain1[,"theta"],
                   mcmc.output$chain2[,"theta"],
                   mcmc.output$chain3[,"theta"])

Puis de calculer l’espérance de vie correspondante :

lambda <- -1/log(theta_samples)

On a ainsi 5100 valeurs simulées dans la distribution a posteriori de $\lambda$ dont les premières sont :

head(lambda)
#> [1] 1.0930355 0.9980286 1.0218130 0.7831809 0.9870770 0.8282083

On peut alors en extraire les résumés usuels :

mean(lambda)
#> [1] 0.9381986
quantile(lambda, probs = c(2.5, 97.5)/100)
#>      2.5%     97.5% 
#> 0.6735811 1.2913724

L’espérance de vie est d’un an approximativement. On peut également visualiser la distribution a posteriori de l’espérance de vie (Figure 3.5) :

lambda %>%
  as_tibble() %>%
  ggplot() +
  geom_histogram(aes(x = value), color = "white") +
  labs(x = "Espérance de vie")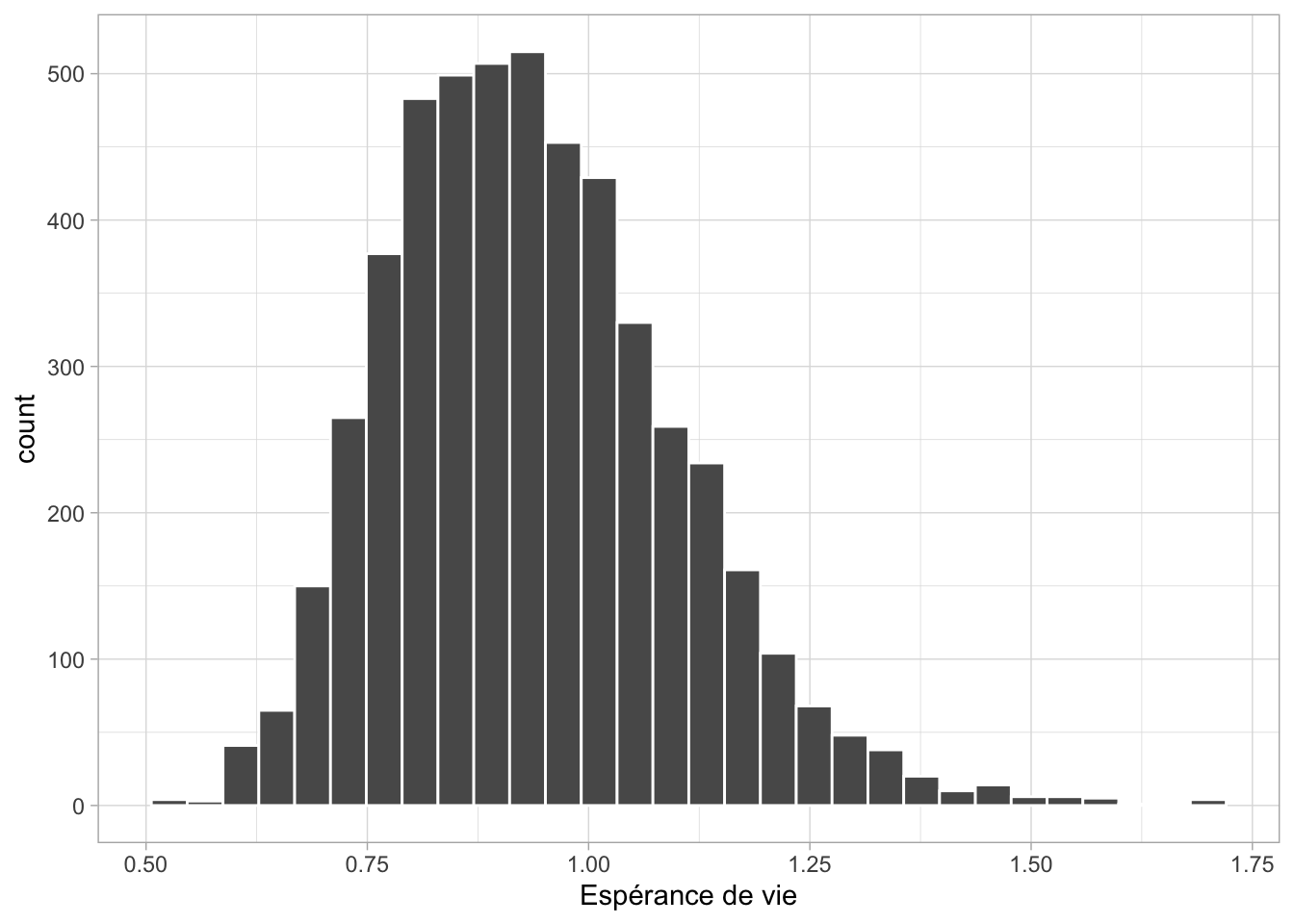

Figure 3.5: Histogramme de la distribution a posteriori de l’espérance de vie.

On pourrait aussi calculer l’espérance de vie en l’insérant directement dans le modèle NIMBLE avec une ligne lambda <- -1/log(theta) et en ajoutant lambda dans la liste des sorties (voir plus loin). La solution exposée ici est particulièrement utile avec de gros modèles ou/et des données volumineuses, car cela permet d’alléger la mémoire utilisée.

Maintenant, vous pouvez vous lancer. Pour plus de commodité, j’ai résumé les étapes ci-dessus dans le bloc ci-dessous. Le flux de travail proposé par nimbleMCMC() vous permet de construire vos modèles et de faire des inférences bayésiennes :

model <- nimbleCode({
  y ~ dbinom(theta, n) # vraisemblance binomiale
  theta ~ dbeta(1, 1) # prior sur la survie
  lambda <- -1/log(theta) # espérance de vie
})
dat <- list(n = 57, y = 19)
par <- c("theta", "lambda")
inits <- function() list(theta = runif(1,0,1))
n.iter <- 5000
n.burnin <- 1000
n.chains <- 3
mcmc.output <- nimbleMCMC(code = model,
                          data = dat,
                          inits = inits,
                          monitors = par,
                          niter = n.iter,
                          nburnin = n.burnin,
                          nchains = n.chains)
MCMCsummary(object = mcmc.output, round = 2)
MCMCplot(object = mcmc.output)
MCMCtrace(object = mcmc.output, pdf = FALSE, ind = TRUE)

J’ai introduit dans cette section le strict minimum pour se lancer avec NIMBLE. Mais NIMBLE est bien plus qu’un simple moteur MCMC, il s’agit d’un environnement de programmation qui vous donne un contrôle total sur la construction de vos modèles et l’estimation des paramètres ; vous pouvez écrire vos propres fonctions et distributions, choisir des méthodes MCMC vous-mêmes, ou même coder vos propres algorithmes ; je vous renvoie vers le manuel https://r-nimble.org/html_manual/cha-welcome-nimble.html pour plus de détails.

3.3 `brms`

brms signifie Bayesian Regression Models using Stan. Ce package permet de formuler et d’estimer des modèles de régression (voir la section suivante et les Chapitres 5 et 6) de manière intuitive grâce à une syntaxe proche de celle du package lme4 (la référence R pour les modèles mixtes), tout en s’appuyant sur Stan, un logiciel de référence en statistique bayésienne. Le package est en constant développement, rendez-vous à https://paul-buerkner.github.io/brms/. Vous pouvez obtenir de l’aide via https://discourse.mc-stan.org/.

Pour utiliser brms, on commence par préparer les données :

dat <- data.frame(y = 19, n = 57)

Sans oublier de charger brms :

library(brms)

La vraisemblance est binomiale dans notre exemple fil rouge. Dans brms, on peut exprimer cela simplement :

bayes.brms <- brm(
  y | trials(n) ~ 1, # le nombre de succès est fonction d'un intercept
  family = binomial("logit"), # famille binomiale avec fonction de lien logit
  data = dat, # données utilisées
  chains = 3, # nombre de chaînes MCMC
  iter = 2000, # nombre total d'itérations par chaîne
  warmup = 300, # nombre d'itérations burn-in
  thin = 1 # pas de sous-échantillonnage (chaque itération est conservée)
)

La syntaxe est relativement simple mais nécessite quelques explications. L’argument y | trials(n) ~ 1 permet de spécifier un modèle dans lequel on a $y$ succès parmi $n$ essais, et on estime une ordonnée à l’origine ou intercept seulement, le 1 après ~. Pourquoi un intercept ici ? Pourquoi pas directement la survie $\theta$ ? Parce qu’on utilise family = binomial("logit") à la ligne d’après pour spécifier à brms que la variable réponse suit une loi binomiale. Autrement dit on a un modèle linéaire généralisé (voir le Chapitre 6) avec $\text{logit}(\theta) = \beta$ et on estime $\beta$ l’intercept. Les arguments iter = 2000, warmup = 300 et chains = 3 stipulent à brms d’utiliser 300 itérations pour l’adaptation (burn-in), et les 1700 suivantes pour l’inférence, avec 3 chaînes.

Jetons un coup d’oeil aux résultats :

summary(bayes.brms)
#>  Family: binomial 
#>   Links: mu = logit 
#> Formula: y | trials(n) ~ 1 
#>    Data: dat (Number of observations: 1) 
#>   Draws: 3 chains, each with iter = 2000; warmup = 300; thin = 1;
#>          total post-warmup draws = 5100
#> 
#> Regression Coefficients:
#>           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept    -0.70      0.28    -1.27    -0.17 1.00     1853     2580
#> 
#> Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Cette commande affiche un tableau récapitulatif des estimations postérieures pour chaque paramètre du modèle. On y trouve :

Estimate est la moyenne a posteriori.
Est.Error est l’écart-type de la distribution a posteriori.
l-95% CI et u-95% CI sont les bornes de l’intervalle de crédibilité à 95%.
Le diagnostic de convergence Rhat.
Bulk_ESS est la taille effective d’échantillon (Tail_ESS est une autre mesure de la taille effective d’échantillon qu’on n’utilisera pas ici).

La moyenne a posteriori vaut -0.7 bien loin de la proportion de ragondins qui ont survécu à l’hiver ($19/57 \approx 0.33$). Comme toujours dans R et l’implémentation des modèles linéaires généralisés (voir Chapitre 6), les estimations des paramètres sont données sur l’échelle de la fonction de lien. Ici l’intercept estimé est exprimé sur l’échelle logit. Pour le convertir en probabilité de survie (entre 0 et 1), on extrait d’abord les valeurs générées dans la distribution a posteriori de l’intercept $\beta$ avec la fonction brms::as_draws_matrix() :

draws_fit <- as_draws_matrix(bayes.brms)

Puis on applique la fonction logistique réciproque plogis() sur chacune de ces valeurs pour obtenir tout un tas de valeurs simulées dans la distribution a posteriori de la survie $\theta$ :

beta <- draws_fit[,'Intercept'] # sélectionne la colonne intercept
theta <- plogis(beta)  # conversion logit -> [0,1]

On obtient ainsi une estimation directe de la moyenne a posteriori de la probabilité de survie, accompagnée de son intervalle de crédibilité à 95% :

mean(theta)
#> [1] 0.3339455
quantile(theta, probas = c(2.5,97.5)/100)
#>        0%       25%       50%       75%      100% 
#> 0.1564688 0.2914508 0.3332220 0.3751883 0.5876202

Ou plus directement avec la fonction posterior::summarise_draws() :

summarise_draws(theta)
#> # A tibble: 1 × 10
#>   variable   mean median     sd    mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>     <dbl>  <dbl>  <dbl>  <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 Intercept 0.334  0.333 0.0614 0.0620 0.235 0.437  1.00    1853.    2580.

Pour visualiser la distribution a posteriori de la probabilité de survie, il suffit d’utiliser (Figure 3.6) :

draws_fit %>%
  ggplot(aes(x = theta)) +
  geom_histogram(color = "white", fill = "steelblue", bins = 30) +
  labs(x = "Probabilité de survie", y = "Fréquence")

$Histogramme de la distribution a posteriori de la probabilité de survie ($\theta$).$

Figure 3.6: Histogramme de la distribution a posteriori de la probabilité de survie ($\theta$).

Dans brms, on peut évaluer la convergence des chaînes MCMC (Figure 3.7) :

plot(bayes.brms)

$Densité a posteriori et trace plot de la probabilité de survie sur l'échelle logit ($\beta$).$

Figure 3.7: Densité a posteriori et trace plot de la probabilité de survie sur l’échelle logit ($\beta$).

Ce graphique affiche les trace plots (à droite) ainsi que les densités a posteriori (à gauche). Au passage, pour déterminer de la longueur de la période de pré-chauffage ou burn-in, il suffit de faire tourner brms avec warmup = 0 pour quelques centaines ou milliers d’itérations et d’examiner la trace du paramètre pour décider du nombre d’itérations à utiliser pour atteindre la convergence.

Un avantage majeur des méthodes MCMC est qu’elles permettent d’obtenir la distribution a posteriori de n’importe quelle fonction des paramètres en appliquant cette fonction aux valeurs tirées dans les distributions a posteriori de ces paramètres. A noter qu’ici on estime l’intercept $\beta$ et on a donc déjà utilisé cette idée pour obtenir la distribution a posteriori de la probabilité de survie en appliquant la fonction logit réciproque. Comme autre exemple, disons que j’aimerais calculer l’espérance de vie des ragondins, celle-ci étant donnée par $\lambda = -1/\log(\theta)$ :

beta <- draws_fit[,'Intercept'] # sélectionne la colonne intercept
theta <- plogis(beta)  # conversion logit -> [0,1]
lambda <- -1 / log(theta) # transforme survie en espérance de vie
summarize_draws(lambda) # résumé des tirages : moyenne, médiane, intervalles
#> # A tibble: 1 × 10
#>   variable   mean median    sd   mad    q5   q95  rhat ess_bulk ess_tail
#>   <chr>     <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
#> 1 Intercept 0.924  0.910 0.160 0.155 0.690  1.21  1.00    1853.    2580.

L’espérance de vie est d’un an approximativement. On peut également visualiser la distribution a posteriori de l’espérance de vie (Figure 3.8) :

lambda %>%
  as_tibble() %>%
  ggplot() +
  geom_histogram(aes(x = Intercept), color = "white") +
  labs(x = "Espérance de vie")

Figure 3.8: Histogramme de la distribution a posteriori de l’espérance de vie.

Il y a tout un tas de paramètres qui sont fixés par défaut dans brms, il est important d’en être conscient. Ça concerne les priors en particulier. Dans brms, les priors par défaut sont souvent non informatifs ou faiblement informatifs, mais il est toujours bon de les examiner explicitement. La commande suivante permet d’afficher le résumé des priors utilisés dans un modèle déjà ajusté :

prior_summary(bayes.brms)
#> Intercept ~ student_t(3, 0, 2.5)

Le package brms utilise comme a priori faiblement informatif une loi de Student à 3 degrés de liberté, centrée en 0, avec un écart-type de 2.5. Les 3 degrés de liberté donnent une distribution avec des queues plus épaisses qu’une normale, ce qui donne une certaine robustesse aux valeurs extrêmes. Le centre en 0 traduit une absence d’a priori fort sur la valeur de l’intercept. La largeur 2.5 autorise une variation raisonnablement large de l’intercept sans être complètement non-informatif.

Dans certains cas, il est pertinent de définir soi-même un prior, par exemple pour refléter des connaissances issues de la littérature ou pour contraindre d’avantage l’estimation (prior informatif). Ici, on propose un prior normal centré en 0 avec un écart-type de 1.5 sur l’intercept, on en reparlera au Chapitre 4 :

nlprior <- prior(normal(0, 1.5), class = "Intercept")

On peut ensuite l’utiliser dans la spécification du modèle :

bayes.brms <- brm(y | trials(n) ~ 1,
                  family = binomial("logit"),
                  data = dat,
                  prior = nlprior, # nos propres priors
                  chains = 3,
                  iter = 2000,
                  warmup = 300,
                  thin = 1)

Vous pouvez vérifier que les résultats sont proches de ceux obtenus avec le prior par défaut :

summary(bayes.brms)
#>  Family: binomial 
#>   Links: mu = logit 
#> Formula: y | trials(n) ~ 1 
#>    Data: dat (Number of observations: 1) 
#>   Draws: 3 chains, each with iter = 2000; warmup = 300; thin = 1;
#>          total post-warmup draws = 5100
#> 
#> Regression Coefficients:
#>           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept    -0.68      0.28    -1.26    -0.15 1.00     1588     1980
#> 
#> Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

3.4 En résumé

NIMBLE permet de modéliser aussi bien des situations simples que des modèles complexes, avec une grande flexibilité.
Sa syntaxe est basée sur R, ce qui facilite sa prise en main si vous connaissez le langage.
Il offre un contrôle total sur le modèle et les algorithmes, mais suppose d’être à l’aise avec la programmation.
À l’inverse, brms permet de tirer parti des méthodes MCMC sans avoir à écrire le modèle soi-même (la vraisemblance en particulier).
Sa syntaxe est simple et proche de celle de lme4, ce qui le rend particulièrement adapté pour les modèles linéaires généralisés (mixtes ou pas ; voir Chapitre 6).
En contrepartie, brms repose sur des composants préprogrammés (familles de modèles, etc.), et il est important d’être attentif aux choix faits par défaut, notamment en ce qui concerne les distributions a priori.
Ce chapitre propose ainsi une première approche concrète de l’implémentation des modèles bayésiens, avant d’aborder des modèles plus riches, comme les modèles mixtes.

2 Les méthodes MCMC

4 Les distributions a priori

Chapitre 3 Mise en oeuvre pratique

3.1 Introduction

3.2 NIMBLE

3.3 brms

3.4 En résumé

3.2 `NIMBLE`

3.3 `brms`