Chapitre 5 La régression

5.1 Introduction

Ce chapitre présente l’application de la statistique bayésienne à la régression linéaire. On prendra un exemple qui nous permettra d’aller un peu plus loin que notre exemple fil rouge sur la survie. Ce sera l’occasion d’aborder comment et pourquoi utiliser un modèle pour simuler des données. Nous en profiterons pour illustrer la comparaison et la validation des modèles. Nous utiliserons NIMBLE et brms et comparerons avec l’approche fréquentiste.

5.2 La régression linéaire

5.2.1 Le modèle

Pour changer un peu, je vous propose d’utiliser NIMBLE et brms sur un exemple différent de celui de l’estimation de la survie. Attardons-nous sur la régression linéaire.

Commençons par poser les bases de notre modèle linéaire. On a \(n\) mesures d’une variable réponse \(y_i\) avec \(i\) qui varie de 1 à \(n\). Pensez par exemple à la masse (en kilogrammes) de nos ragondins dans l’exemple fil rouge. On associe chaque mesure à une variable explicative \(x_i\), par exemple la température extérieure moyenne en hiver (en degrés Celsius) pour nos ragondins. On cherche à étudier l’effet de la température sur la masse. Le plus simple est de supposer une relation linéaire entre les deux, on utilise donc un modèle de régression linéaire. Le modèle comporte une ordonnée à l’origine (ou intercept) \(\beta_0\), et une pente \(\beta_1\) qui décrit l’effet de \(x_i\) sur \(y_i\), ou de la température sur la masse des ragondins. On a aussi besoin d’un paramètre pour décrire la variabilité résiduelle représentée par un paramètre de variance \(\sigma^2\), qui capte la part de variation dans les \(y_i\) non expliquée par les \(x_i\). Vous avez probablement déjà rencontré ce modèle sous la forme : \(y_i = \beta_0 + \beta_1 x_i + \varepsilon_i\) où les erreurs \(\varepsilon_i\) sont supposées indépendantes et distribuées selon une loi normale de moyenne 0 et de variance \(\sigma^2\).

L’intercept \(\beta_0\) nous donne la masse quand la température est de 0 degré (\(x_i = 0\)). Le paramètre \(\beta_1\) nous renseigne sur le changement dans la variable réponse pour une augmentation d’une unité (ici 1 degré Celsius) de la variable explicative (d’où le terme “pente” pour désigner ce paramètre). En général, on conseille (fortement) de centrer (soustraire la moyenne) et réduire (diviser par l’écart-type) les valeurs de la variable explicative pour des questions numériques et d’interprétation. Numérique d’abord car cela permet aux algorithmes, qu’ils soient fréquentistes ou bayésiens, de ne pas se perdre dans des recoins de l’espace du paramètre. Interprétation ensuite, car on interprète alors l’intercept \(\beta_0\) comme la valeur de la variable réponse pour une valeur moyenne de la variable explicative.

Dans cette section, plutôt que d’analyser de “vraies” données, nous allons, à partir des paramètres \(\beta_0\), \(\beta_1\) et \(\sigma\), simuler des données artificielles, comme si elles provenaient d’un vrai processus sous-jacent.

5.2.2 Simuler des données

Qu’est-ce que j’entends par simuler des données ? L’analyse et la simulation des données sont deux faces d’un même modèle. Dans l’analyse, on utilise les données pour estimer les paramètres d’un modèle. Dans la simulation, on fixe les paramètres et on utilise le modèle pour générer des données. Une raison d’utiliser les simulations est que cette gymnastique va nous obliger à bien comprendre le modèle ; si je n’arrive pas à simuler des données à partir d’un modèle, c’est que je n’ai pas complètement compris comment il marchait. Il y a des tas d’autres bonnes raisons pour utiliser les simulations. Comme la vérité (les paramètres et le modèle) est connue, on peut vérifier que le modèle est bien codé. On peut évaluer le biais et la précision des estimations de nos paramètres, évaluer les effets de ne pas respecter les hypothèses du modèle, planifier un protocole de récolte de données ou encore évaluer la puissance d’un test statistique. Bref, c’est une technique très utile à avoir dans votre boîte à outils !

Revenons à notre exemple. Pour simuler des données selon le modèle de régression linéaire, on commence par fixer nos paramètres : \(\beta_0 = 0.1\), \(\beta_1 = 1\) et \(\sigma^2 = 0.5\) :

beta0 <- 0.1 # valeur vraie de l'intercept
beta1 <- 1 # valeur vraie du coefficient de x
sigma <- 0.5 # écart-type des erreurs

Puis on simule \(n = 100\) valeurs \(x_i\) de notre variable explicative selon une loi normale de moyenne 0 et d’écart-type 1, autrement dit \(N(0,1)\) :

set.seed(666) # pour rendre la simulation reproductible
n <- 100 # nombre d'observations
x <- rnorm(n = n, mean = 0, sd = 1) # covariable x simulée selon une loi normale standard

Enfin, on simule les valeurs de la variable réponse, en ajoutant une erreur normale epsilon à la relation linéaire beta0 + beta1 * x :

epsilon <- rnorm(n, mean = 0, sd = sigma) # génère les erreurs normales
y <- beta0 + beta1 * x + epsilon # ajoute les erreurs à la relation linéaire
data <- data.frame(y = y, x = x)

La Figure 5.1 ci-dessous montre les données simulées, ainsi que la droite de régression correspondant au modèle utilisé pour les générer :

Figure 5.1: Données simulées (n = 100) selon le modèle \(y_i = \beta_0 + \beta_1 x_i + \varepsilon_i\), avec \(\beta_0 = 0.1\), \(\beta_1 = 1\) et \(\sigma = 1\). La droite rouge correspond à la droite de régression.

5.2.3 L’ajustement avec brms

Dans cette section, on utilise brms pour ajuster le modèle de régression linéaire aux données qu’on vient de générer. Si tout se passe bien, les paramètres estimés devraient être proches des valeurs utilisées pour générer les données. Je vais relativement vite ici puisqu’on a couvert les différentes étapes au Chapitre 3. La syntaxe est très proche de celle qu’on utiliserait pour ajuster le modèle par maximum de vraisemblance avec la fonction lm() dans R :

lm.brms <- brm(y ~ x, # formule : y en fonction de x
               data = data, # jeu de données
               family = gaussian) # distribution normale

Jetons un coup d’oeil aux résumés numériques et aux diagnostics de convergence :

summary(lm.brms)
#>  Family: gaussian 
#>   Links: mu = identity; sigma = identity 
#> Formula: y ~ x 
#>    Data: data (Number of observations: 100) 
#>   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 4000
#> 
#> Regression Coefficients:
#>           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept     0.06      0.06    -0.05     0.17 1.00     4138     3110
#> x             1.10      0.06     0.99     1.21 1.00     3735     3192
#> 
#> Further Distributional Parameters:
#>       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma     0.57      0.04     0.49     0.66 1.00     3951     2849
#> 
#> Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Par défaut, brms a utilisé 4 chaînes qui ont tourné pendant 2000 itérations chacune avec 1000 itérations utilisées comme burn-in, soit au total 4000 itérations pour l’inférence a posteriori. Dans les sorties, Intercept, x et sigma correspondent respectivement aux paramètres \(\beta_0\), \(\beta_1\) et \(\sigma\) du modèle. Le \(\hat{R}\) pour les 3 paramètres vaut 1, et les tailles d’échantillon efficaces sont satisfaisantes. Les intervalles de crédibilité contiennent la vraie valeur du paramètre utilisée pour simuler les données.

On vérifie que le mixing est bon (Figure 5.2) :

plot(lm.brms)

Figure 5.2: Histogrammes des distributions a posteriori (colonne de gauche) et traces (colonne de droite) des paramètres de la régression linéaire.

5.2.4 Des priors faiblement informatifs

Plutôt que d’utiliser les priors par défaut de brms, choisissons d’autres priors. Nous allons utiliser des priors faiblement informatifs, et plus spécifiquement une normale avec moyenne 0 et écart-type 1.5 ou \(N(0,1.5)\) pour les paramètres de régression \(\beta_0\) et \(\beta_1\). On a déjà parlé des priors faiblement informatifs au Chapitre 4. L’idée est proche de celle des priors vagues ou non-informatifs, dans le sens où l’on s’efforce de refléter via les priors faiblement informatifs le fait qu’on n’a pas vraiment d’information sur les paramètres du modèle. La différence est que les priors non-informatifs peuvent induire des valeurs aberrantes comme on l’a vu au Chapitre 4. C’est encore le cas ici. Prenez par exemple des \(N(0,100)\) pour les paramètres de la relation linéaire qui lie la masse des ragondins à la température, et simulez tout un tas de valeurs dans ces priors, puis formez la relation linéaire :

# nombre de droites à simuler
n_lines <- 100

# tirages des intercepts et pentes selon les priors
intercepts <- rnorm(n_lines, mean = 0, sd = 100)
slopes <- rnorm(n_lines, mean = 0, sd = 100)

# création d'un data frame
lines_df <- data.frame()
for (i in 1:n_lines) {
  y_vals <- intercepts[i] + slopes[i] * x
  temp_df <- data.frame(x = x, y = y_vals, line = as.factor(i))
  lines_df <- rbind(lines_df, temp_df)
}

# tracé avec ggplot2
ggplot(lines_df, aes(x = x, y = y, group = line)) +
  geom_line(alpha = 0.3) +
  theme_minimal() +
  labs(x = "x", y = "y")

Figure 5.3: Simulation de droites de régression issues des distributions a priori. Chaque ligne correspond à un tirage des paramètres : intercept et pente ~ N(0, 100).

On voit dans la Figure 5.3 qu’on obtient des valeurs aberrantes pour les \(y_i\), avec des ragondins de plus de 400 kilogrammes, et des valeurs (très) négatives pour la masse. On vient de faire un “prior predictive check”, comme au Chapitre 4. Dans la Figure 5.4, on fait la même chose avec notre prior faiblement informatif \(N(0,1.5)\) :

Figure 5.4: Simulation de droites de régression issues des distributions a priori. Chaque ligne correspond à un tirage des paramètres : intercept et pente ~ N(0, 1.5).

On obtient des valeurs plus raisonnables pour la masse des ragondins qui dépassent rarement 10 kilogrammes. On a toujours des valeurs négatives, mais moindres, l’algorithme MCMC devrait s’en sortir. Il y a aussi un avantage numérique à utiliser des priors faiblement informatifs, ils aident les méthodes MCMC à ne pas se perdre dans l’espace de toutes les valeurs possibles pour les paramètres à estimer, et leur permettent de se focaliser sur les valeurs réalistes de ces paramètres. En faisant ça, vous avez peut-être l’impression qu’on utilise les données pour construire les priors, alors qu’on a dit que le prior devait refléter l’information disponible avant de voir les données. C’est l’occasion de préciser un peu ce point. L’important est surtout que le prior représente l’information indépendante des données qui sont utilisées dans la vraisemblance.

On s’est jusqu’ici concentrés sur les paramètres de régression, l’intercept \(\beta_0\) et la pente \(\beta_1\). Mais qu’en est-il de l’écart-type, \(\sigma\) ? Ce paramètre est tout aussi important : il reflète à quel point les observations s’écartent de la tendance moyenne décrite par la droite de régression.

Une option souvent envisagée est de lui attribuer une loi uniforme, par exemple \(\sigma \sim U(0, B)\), avec une borne inférieure naturelle (0, puisque \(\sigma\) est toujours positive), mais une borne supérieure \(B\) difficile à choisir. Quelle valeur maximale donner à un écart-type ? Dans certains cas, une valeur apparemment raisonnable peut se révéler trop large. Par exemple, si l’on modélise des tailles humaines et que l’on fixe \(\sigma \sim U(0, 50)\) (en cm), cela revient à supposer que 95% des tailles sont réparties sur une plage de 100 cm autour de la moyenne – ce qui est très improbable.

Une alternative plus souple et plus réaliste consiste à utiliser une loi exponentielle \(\sigma \sim \exp(\lambda)\) où \(\lambda > 0\) est un paramètre de taux. Cette loi est définie uniquement pour des valeurs positives, ce qui est cohérent avec la nature de \(\sigma\), et elle favorise les petites valeurs d’écart-type tout en laissant la possibilité à \(\sigma\) d’être plus grande si les données le justifient.

Par défaut, on prend souvent \(\lambda = 1\). Avec \(\lambda = 1\), la moyenne et l’écart-type de cette loi sont tous deux égaux à \(1\), ce qui induit une loi a priori modeste mais non restrictive (Figure 5.5).

Figure 5.5: Comparaison entre deux lois a priori pour l’écart-type \(\sigma\) : une loi uniforme \(\text{U}(0,5)\), qui donne la même densité entre 0 et 5, et une loi exponentielle \(\text{Exp}(1)\), qui favorise les petites valeurs tout en conservant une queue plus lourde.

On peut formaliser ce modèle comme suit : \[\begin{align} y_i &\sim \text{Normale}(\mu_i, \sigma^2) &\text{[vraisemblance]}\\ \mu_i &= \beta_0 + \beta_1 \; x_i &\text{[relation linéaire]}\\ \beta_0, \beta_1 &\sim \text{Normale}(0, 1.5) &\text{[prior sur les paramètres]} \\ \sigma &\sim \text{Exp}(1) &\text{[prior sur les paramètres]} \\ \end{align}\]

Spécifions ces priors :

myprior <- c(
  prior(normal(0, 1.5), class = b), # prior sur le coefficient de x
  prior(normal(0, 1.5), class = Intercept), # prior sur l'intercept
  prior(exponential(1), class = sigma) # prior sur l'écart-type de l'erreur
)

Puis refaisons l’ajustement avec brms :

lm.brms <- brm(y ~ x, 
               data = data, 
               family = gaussian, 
               prior = myprior)

On vérifie que les résumés numériques obtenus sont proches de ceux obtenus avec les priors par défaut, et surtout des valeurs utilisées pour simuler les données :

summary(lm.brms)
#>  Family: gaussian 
#>   Links: mu = identity; sigma = identity 
#> Formula: y ~ x 
#>    Data: data (Number of observations: 100) 
#>   Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
#>          total post-warmup draws = 4000
#> 
#> Regression Coefficients:
#>           Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept     0.06      0.06    -0.06     0.18 1.00     3648     2815
#> x             1.10      0.06     0.99     1.20 1.00     3778     2918
#> 
#> Further Distributional Parameters:
#>       Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma     0.57      0.04     0.49     0.66 1.00     3555     2593
#> 
#> Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).

Ici, les deux modèles donnent quasiment la même chose, ce qui n’a rien de surprenant car les données sont suffisamment informatives pour qu’elles “prennent le dessus sur” le prior. L’intérêt des priors faiblement informatifs ne se voit pas tant dans ce petit exemple que dans d’autres situations : ils évitent les valeurs aberrantes, stabilisent les calculs MCMC et restent utiles quand on a moins de données ou des modèles plus complexes.

5.2.5 L’ajustement avec NIMBLE

On commence par écrire le modèle :

model <- nimbleCode({
  # les priors
  beta0 ~ dnorm(0, sd = 1.5) # prior normal sur l'intercept
  beta1 ~ dnorm(0, sd = 1.5) # prior normal sur le coefficient
  sigma ~ dexp(1) # prior exponentiel sur l'écart-type
  # la vraisemblance
  for(i in 1:n) {
    y[i] ~ dnorm(beta0 + beta1 * x[i], sd = sigma) # equiv de yi = beta0 + beta1 * xi + epsiloni
  }
})

Dans ce bloc de code, on commence par spécifier des priors sur les trois paramètres du modèle : un prior normal centré en 0 avec un écart-type de 1.5 pour l’intercept \(\beta_0\) et pour la pente \(\beta_1\), ainsi qu’un prior exponentiel pour l’écart-type \(\sigma\) des erreurs. La partie suivante est une boucle for(i in 1:n) qui définit la vraisemblance. On spécifie la vraisemblance observation par observation, NIMBLE en déduit automatiquement le produit des vraisemblances sur tous les individus, ce qui correspond à la vraisemblance du jeu de données. Pour chaque observation \(i\), on a une distribution normale centrée en beta0 + beta1 * x[i], avec un écart-type sigma. On retrouve la relation \(y_i = \beta_0 + \beta_1 x_i + \varepsilon_i\) où \(\varepsilon_i \sim N(0,\sigma^2)\) qui est strictement équivalente à \(y_i \sim N(\beta_0 + \beta_1 x_i,\sigma^2)\).

Les étapes suivantes consistent à mettre les données dans une liste, spécifier les valeurs initiales, et préciser les paramètres pour lesquels on souhaite des sorties :

dat <- list(x = x, y = y, n = n) # données
inits <- list(list(beta0 = -0.5, beta1 = -0.5, sigma = 0.1), # valeurs initiales chaine 1
              list(beta0 = 0, beta1 = 0, sigma = 1), # valeurs initiales chaine 2
              list(beta0 = 0.5, beta1 = 0.5, sigma = 0.5)) # valeurs initiales chaine 3
par <- c("beta0", "beta1", "sigma")

On a alors tous les ingrédients pour lancer NIMBLE :

lm.nimble <- nimbleMCMC(
  code = model,
  data = dat,
  inits = inits,
  monitors = par,
  niter = 2000,
  nburnin = 1000,
  nchains = 3
)

Inspectons les résultats :

MCMCsummary(lm.nimble, round = 2)
#>       mean   sd  2.5%  50% 97.5% Rhat n.eff
#> beta0 0.06 0.06 -0.05 0.06  0.17 1.00  3000
#> beta1 1.10 0.06  0.99 1.10  1.21 1.00  3000
#> sigma 0.57 0.04  0.49 0.56  0.65 1.01   772

On retrouve des résumés numériques proches de ceux obtenus avec brms, et proches des vraies valeurs des paramètres utilisés pour simuler les données.

Concernant la convergence, on peut inspecter les trace plots :

MCMCtrace(object = lm.nimble,
          pdf = FALSE,
          ind = TRUE,
          Rhat = TRUE,
          n.eff = TRUE)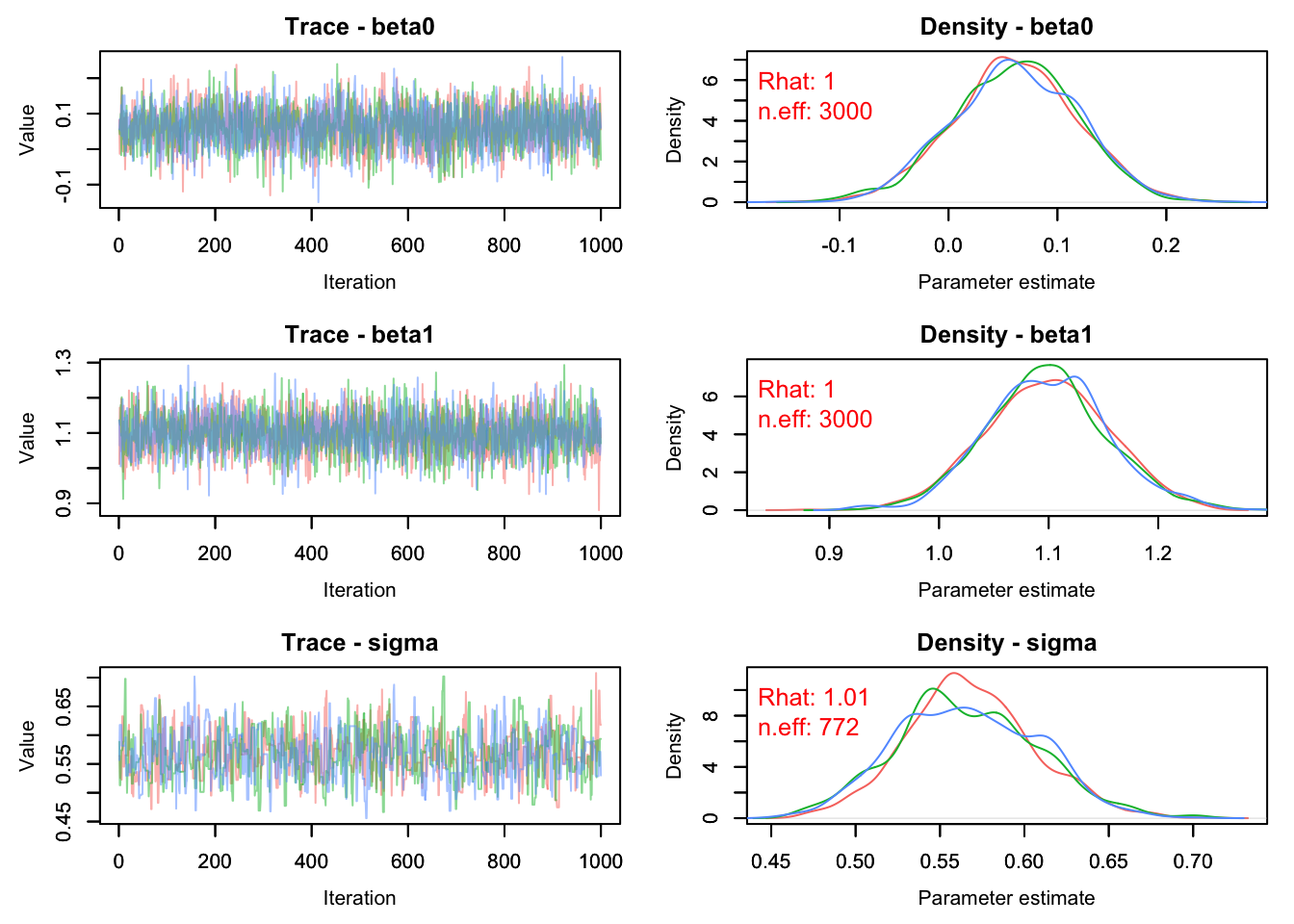

Tout va bien. Le mélange est correct, les diagnostics de convergence sont au vert.

5.2.6 L’ajustement par maximum de vraisemblance

Et pour finir, on peut comparer avec l’ajustement par maximum de vraisemblance qu’on obtient simplement avec la commande lm(y ~ x, data = data), tout est dans la Figure 5.6 :

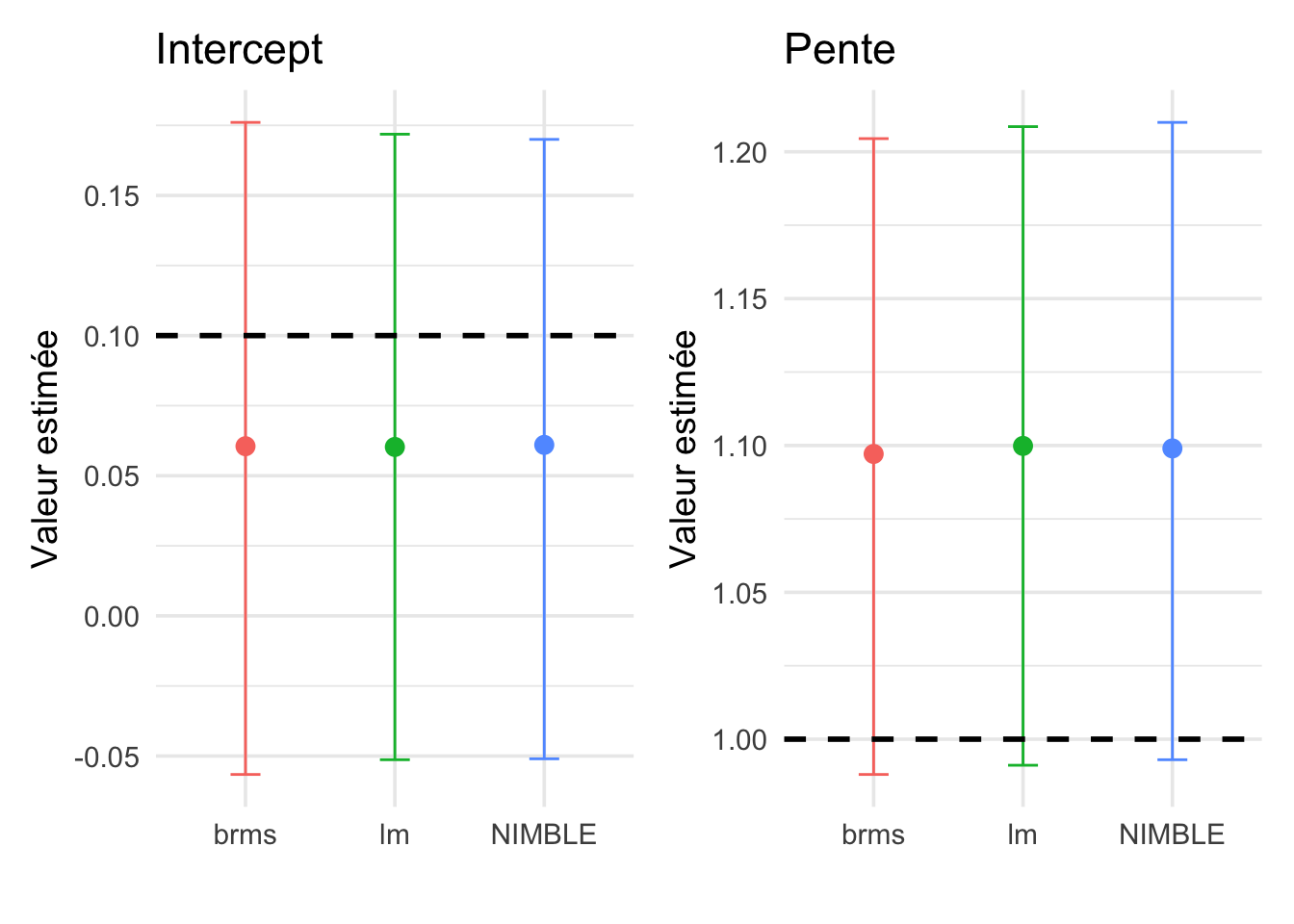
Figure 5.6: Comparaison des estimations des paramètres du modèle (intercept ou ordonnée à l’origine et pente) selon les différentes méthodes (brms, lm et NIMBLE). Les points donnent les moyennes a posteriori pour brms et NIMBLE, et l’estimation du maximum de vraisemblance pour lm. On donne également les intervalles de crédibilité (pour brms et NIMBLE) et de confiance (pour lm) à 95%. La ligne en tirets noirs indique la vraie valeur utilisée pour simuler les données.

Les moyennes a posteriori obtenues avec NIMBLE et brms sont proches des estimations par maximum de vraisemblance pour l’incercept et la pente, dans une moindre mesure. Les intervalles de crédibilité obtenus avec NIMBLE et brms et l’intervalle de confiance obtenu par maximum de vraisemblance englobent tous les vraies valeurs des paramètres qui ont servi à simuler les données. Gardez à l’esprit qu’il s’agit d’une seule simulation, il faudrait répéter l’exercice un grand nombre de fois pour évaluer formellement la distance entre les vraies valeurs et les estimations des paramètres (le biais).

5.3 L’évaluation des modèles

La qualité de l’ajustement d’un modèle aux données est essentielle pour évaluer la confiance que l’on peut accorder aux estimations des paramètres. Les tests de qualité d’ajustement (ou goodness-of-fit en anglais) sont bien établis en statistique fréquentiste, et beaucoup d’entre eux peuvent aussi être utilisés dans des modèles bayésiens simples. C’est le cas par exemple de l’analyse des résidus.

Dans le cas d’une régression linéaire, il y a plusieurs hypothèses sur lesquelles repose le modèle. Ce sont les hypothèses d’indépendance, de normalité, de linéarité et d’homoscédasticité (\(\sigma\) ne varie pas avec la variable explicative). On peut en général évaluer les deux premières avec le contexte. Concernant les deux autres, on peut visualiser l’ajustement en superposant la droite de régression estimée au nuage de points observés. Avec le package brms, cela donne la Figure 5.7 :

# extrait les valeurs tirées dans les distributions a posteriori des paramètres
post <- as_draws_df(lm.brms)

# crée une grille de x pour tracer l'intervalle de crédibilité
grille_x <- tibble(x = seq(min(data$x), max(data$x), length.out = 100))

# pour chaque x, simule des valeurs de y à partir des échantillons
pred <- post %>%
  select(b_Intercept, b_x) %>%
  expand_grid(grille_x) %>%
  mutate(y = b_Intercept + b_x * x) %>%
  group_by(x) %>%
  summarise(
    mean = mean(y),
    lower = quantile(y, 0.025),
    upper = quantile(y, 0.975),
    .groups = "drop"
  )

# droite "vraie" (rouge) sur la même grille
true_line <- grille_x %>%
  mutate(y = beta0 + beta1 * x)

# extrait les moyennes a posteriori des paramètres
intercept <- summary(lm.brms)$fixed[1,1]
slope <- summary(lm.brms)$fixed[2,1]

# tracé
ggplot(data, aes(x = x, y = y)) +
  geom_point(alpha = 0.6) +
  geom_ribbon(data = pred, aes(x = x, ymin = lower, ymax = upper), fill = "blue", alpha = 0.2, inherit.aes = FALSE) +
  geom_line(data = pred, aes(x = x, y = mean), color = "blue", size = 1.2) +
#  geom_line(data = true_line, aes(x = x, y = y), color = "red", size = 1.2) +
  labs(x = "x", y = "y") +
  coord_cartesian(xlim = range(grille_x$x)) +
  theme_minimal()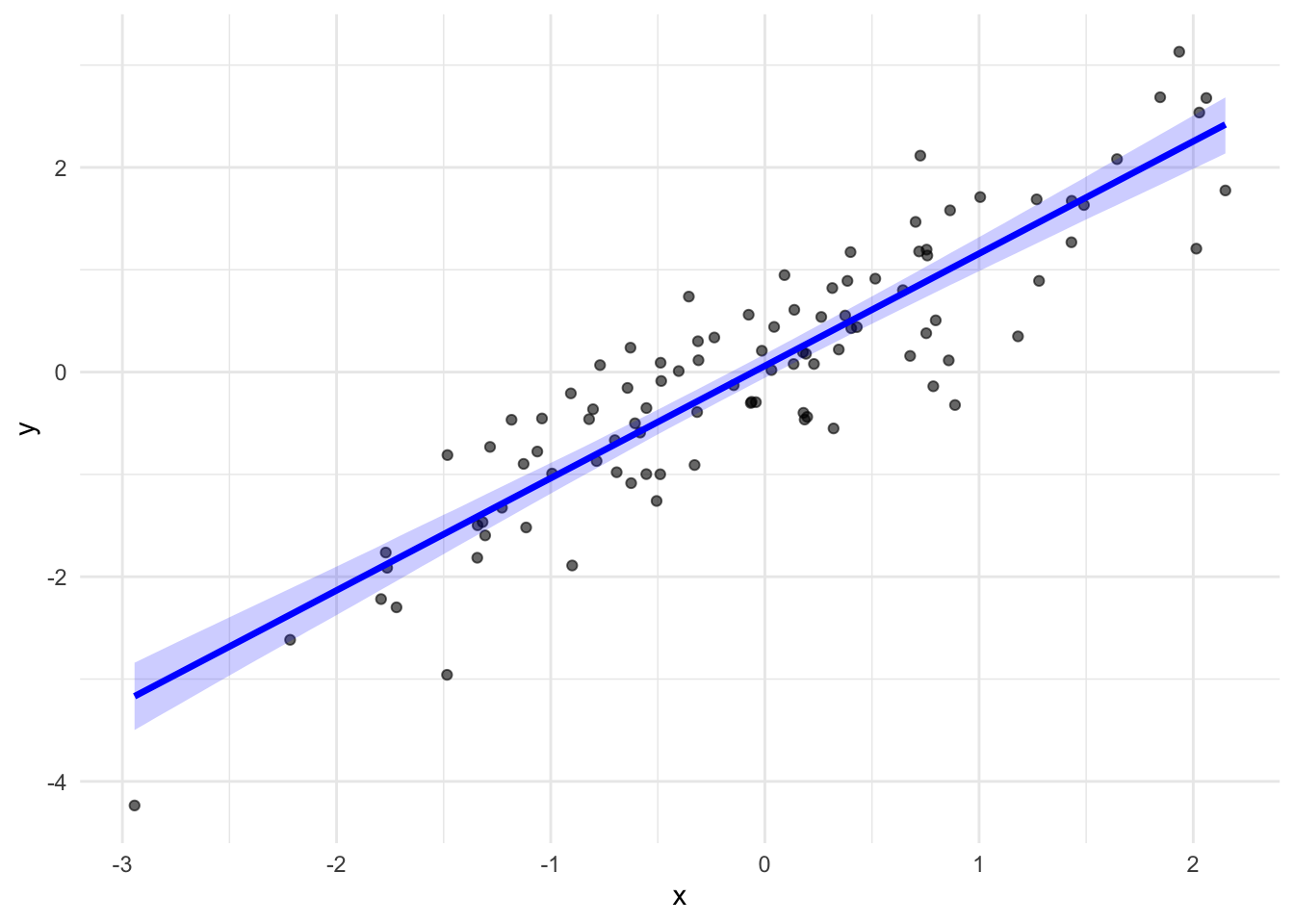

Figure 5.7: Ajustement du modèle linéaire par brms. La droite bleue est la régression estimée, obtenue en fixant l’ordonnée à l’origine et la pente à leur moyenne a posteriori, entourée de son intervalle de crédibilité à 95 %.

Avec NIMBLE, c’est la Figure 5.8 :

# données simulées
x <- data$x
y <- data$y

# tirages postérieurs
posterior <- rbind(lm.nimble$chain1, lm.nimble$chain2, lm.nimble$chain3)
beta0 <- posterior[,'beta0']
beta1 <- posterior[,'beta1']

# grille d'abscisses
x_seq <- seq(min(data$x), max(data$x), length.out = 100)

# calcul des prédictions pour chaque x
pred_matrix <- sapply(x_seq, function(xi) beta0 + beta1 * xi)

# résumé (moyenne et intervalle)
pred_df <- tibble(
  x = x_seq,
  y_mean = colMeans(pred_matrix),
  y_lower = apply(pred_matrix, 2, quantile, probs = 0.025),
  y_upper = apply(pred_matrix, 2, quantile, probs = 0.975)
)

# données et vraie relation
true_df <- tibble(x = x_seq, y_true = 0.1 + 1 * x_seq)

# tracé
ggplot() +
  geom_point(data = data, aes(x = x, y = y), alpha = 0.6) +
  geom_ribbon(data = pred_df, aes(x = x, ymin = y_lower, ymax = y_upper), fill = "blue", alpha = 0.2) +
  geom_line(data = pred_df, aes(x = x, y = y_mean), color = "blue", size = 1.2) +
 # geom_line(data = true_df, aes(x = x, y = y_true), color = "red", size = 1.2) +
  labs(x = "x", y = "y") +
  theme_minimal()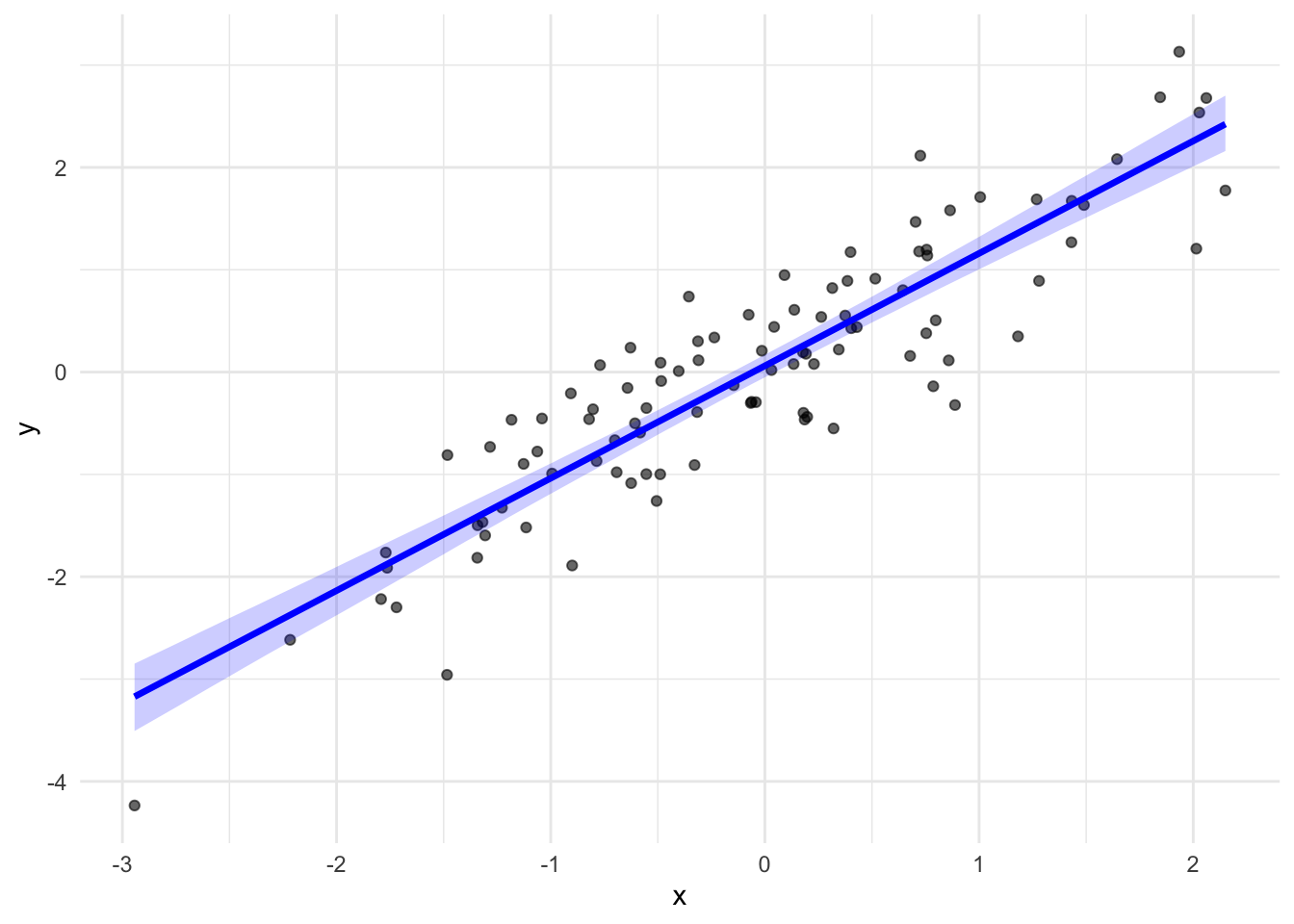

Figure 5.8: Ajustement du modèle linéaire par NIMBLE. La droite bleue est la régression estimée, obtenue en fixant l’ordonnée à l’origine et la pente à leur moyenne a posteriori, entourée de son intervalle de crédibilité à 95 %.

Les méthodes bayésiennes sont souvent utilisées pour des modèles plus complexes que la régression linéaire (comme les modèles mixtes, voir Chapitre 6), pour lesquels il n’existe pas de tests de qualité d’ajustement standards “clé en main”. Dans ces situations, on utilise couramment ce qu’on appelle des posterior predictive checks. L’idée est de simuler de nouveaux jeux de données à partir de la distribution a posteriori des paramètres du modèle, puis de les comparer aux données observées. Plus les données simulées ressemblent aux données réelles, plus cela suggère que le modèle s’ajuste bien. Cette comparaison peut se faire de manière visuelle ou à l’aide d’une Bayesian p-value qui quantifie l’écart entre données simulées et observées.

Dans brms, il suffit de faire :

pp_check(lm.brms)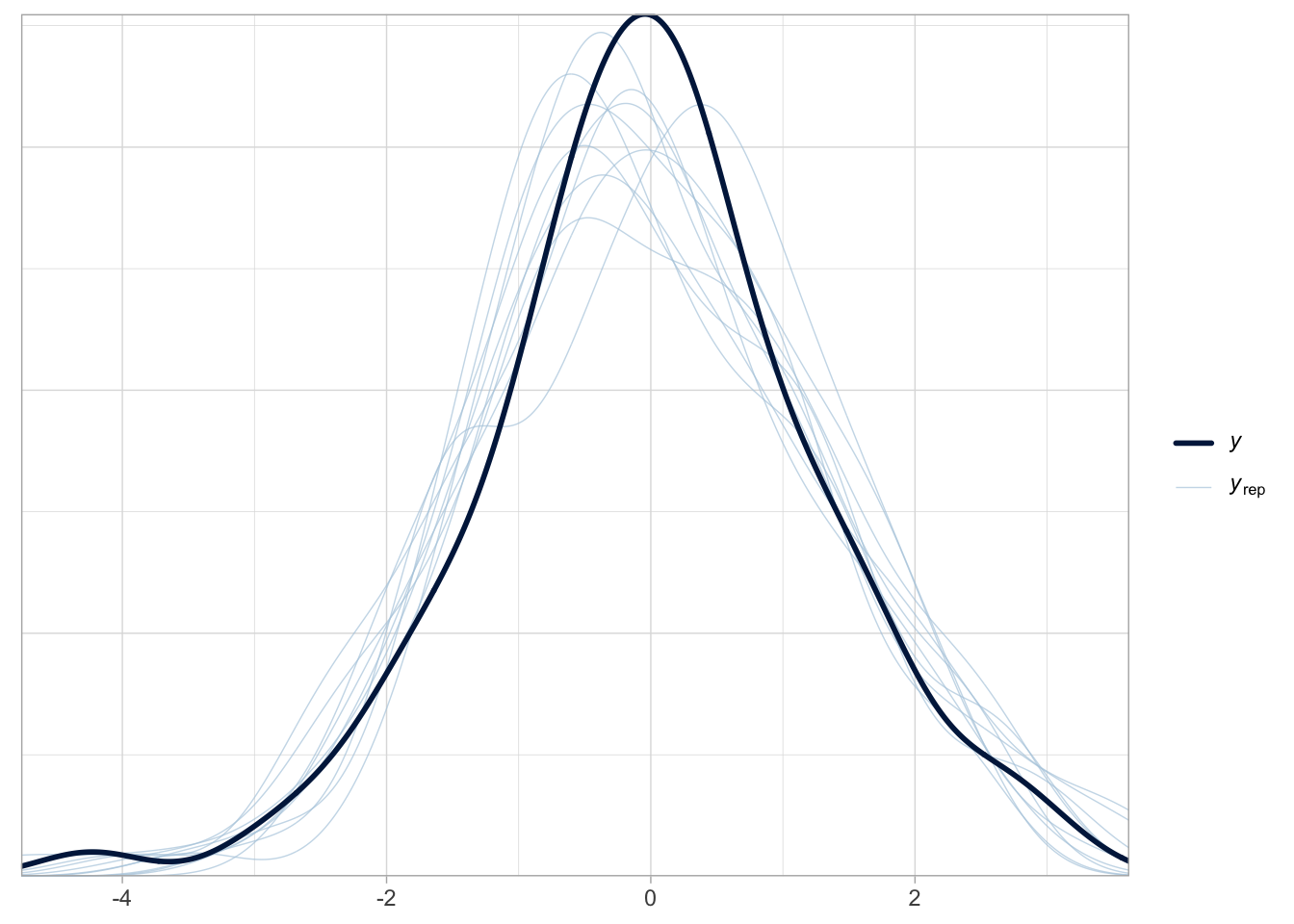

Figure 5.9: Posterior predictive checks réalisés avec brms. La courbe noire correspond aux données observées, les courbes bleues aux données simulées selon le modèle.

La fonction pp_check() génère des graphiques de posterior predictive checks (Figure 5.9). Elle compare les données observées à des données simulées à partir du modèle ajusté. Si le modèle est bien ajusté aux données, alors on devrait pouvoir l’utiliser pour générer des données qui ressemblent aux données observées. Par conséquent, si les courbes simulées recouvrent bien les observations, cela indique que le modèle capte correctement la structure des données. Dans le cas contraire, cela peut suggérer un problème de spécification du modèle, par exemple un lien ou une famille de distribution inadaptée (voir Chapitre 6).

Il n’y a pas de fonction dédiée dans NIMBLE donc il va falloir simuler des données selon le modèle avec les paramètres estimés. On pourrait le faire à la main comme avec l’espérance de vie, mais le plus simple est d’inclure une ligne supplémentaire dans le code NIMBLE :

model <- nimbleCode({
  beta0 ~ dnorm(0, sd = 1.5) # prior normal sur l'intercept
  beta1 ~ dnorm(0, sd = 1.5) # prior normal sur le coefficient
  sigma ~ dexp(1) # prior exponentiel sur l'écart-type
  for(i in 1:n) {
    y[i] ~ dnorm(beta0 + beta1 * x[i], sd = sigma) # modèle pour les données observées
    y_sim[i] ~ dnorm(beta0 + beta1 * x[i], sd = sigma) # modèle pour les données simulées
  }
})

C’est la ligne y_sim[i] ~ dnorm(beta0 + beta1 * x[i], sd = sigma) que j’ai ajoutée pour simuler selon le modèle ajusté. Les données et les valeurs initiales ne changent pas, il nous faut juste ajouter y_sim à la liste des paramètres qu’on veut retrouver dans les sorties :

par <- c("beta0", "beta1", "sigma", "y_sim")

Puis on relance NIMBLE :

lm.nimble <- nimbleMCMC(
  code = model,
  data = dat,
  inits = inits,
  monitors = par,
  niter = 2000,
  nburnin = 1000,
  nchains = 3
)
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|

On fusionne alors les 3 chaînes, puis on sélectionne uniquement les colonnes correspondant à y_sim :

# fusion des trois chaînes MCMC obtenues avec NIMBLE
y_sim_mcmc <- rbind(lm.nimble$chain1, lm.nimble$chain2, lm.nimble$chain3)
# sélection des colonnes correspondant aux simulations de y (les y_sim[i])
y_sim_cols <- grep("^y_sim\\[", colnames(y_sim_mcmc))
# extraction de la matrice des valeurs simulées pour y
y_sim_matrix <- y_sim_mcmc[, y_sim_cols]

On fait ensuite 10 tirages, comme par défaut dans brms, puis on met les résultats en forme :

# fixe la graine pour reproductibilité
set.seed(123)
# sélectionne au hasard 10 tirages parmi les simulations (comme le fait brms par défaut)
sim_indices <- sample(1:nrow(y_sim_matrix), 10)
# mise en forme des simulations 
simulations_df <- data.frame(
  y_sim = as.vector(t(y_sim_matrix[sim_indices, ])), # valeurs simulées
  Replicate = rep(1:length(sim_indices), each = n), # identifiant du tirage (1 à 10)
  Observation = rep(1:n, times = length(sim_indices)) # identifiant de l'observation (1 à n)
)

Enfin, on obtient le graphe des posterior predictive checks dans la Figure 5.10 :

ggplot() +
  geom_density(aes(x = y_sim, group = Replicate), color = "lightblue", alpha = 0.2, data = simulations_df) +
  geom_density(aes(x = y), color = "black", alpha = 0.5, size = 1.2, data = data.frame(y = y)) +
  labs(x = "",
       y = "") +
  theme_minimal(base_size = 14)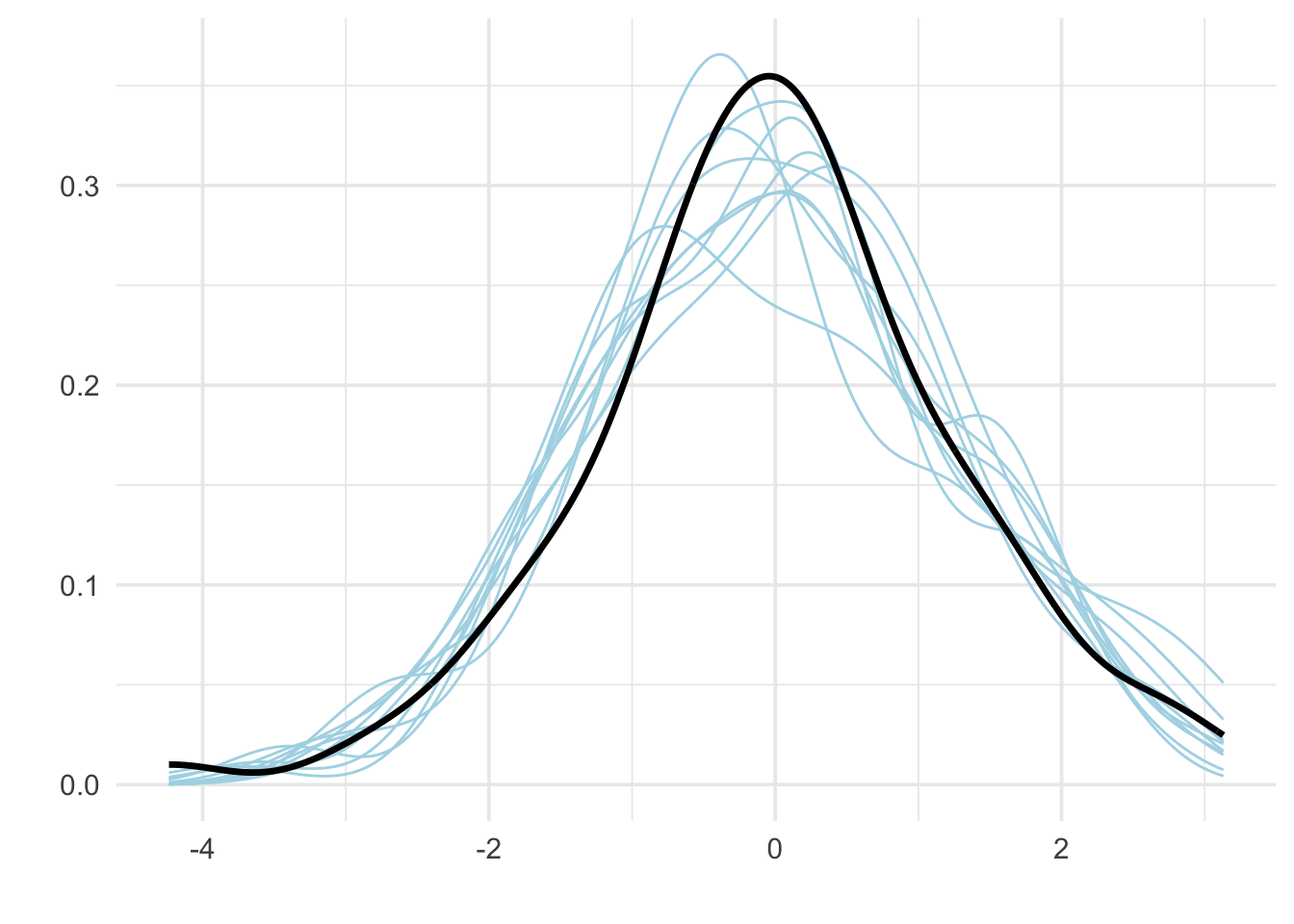

Figure 5.10: Posterior predictive checks réalisés avec NIMBLE. La courbe noire correspond aux données observées, les courbes bleues aux données simulées selon le modèle.

On peut également calculer une Bayesian p-value (ou p-valeur bayésienne) qui représente la proportion de jeux de données simulés sous le modèle pour lesquels la statistique choisie (ici la moyenne) est aussi grande ou plus grande que celle observée. Une valeur proche de 0 ou de 1 peut indiquer un mauvais ajustement du modèle pour cette statistique particulière, tandis qu’une valeur proche de 0.5 suggère un bon ajustement. Cette Bayesian p-value s’obtient comme suit :

# Statistique de test observée : ici la moyenne des y observés
T_obs <- mean(y)

# Statistique de test sur les données simulées
T_sim <- apply(y_sim_matrix, 1, mean)

# Valeur-p bayésienne : proportion des simulations où T_sim est plus extrême que T_obs
bayes_pval <- mean(T_sim >= T_obs)

# Affichage du résultat
bayes_pval
#> [1] 0.512

Avec brms, on peut aussi obtenir cette Bayesian p-value :

# Extraire les simulations de y_rep
y_rep <- posterior_predict(lm.brms)

# Calculer la statistique de test sur les données simulées (moyenne ici)
T_sim <- rowMeans(y_rep)

# Calculer la statistique observée
T_obs <- mean(lm.brms$data$y)

# Calculer la Bayesian p-value
bayes_pval <- mean(T_sim >= T_obs)

# Afficher le résultat
bayes_pval
#> [1] 0.493

5.4 La comparaison de modèles

Comme on l’a vu dans le Chapitre 1, la statistique bayésienne permet de comparer plusieurs hypothèses entre elles, et de savoir à quel point une hypothèse est plausible à partir des données que nous avons collectées.

Il est essentiel, avant de comparer des modèles, de se demander quel est l’objectif de l’analyse : s’agit-il de mieux comprendre un phénomène (approche explicative), ou plutôt de faire des prédictions (approche prédictive) ?

Une stratégie consiste à construire un modèle unique incluant les variables jugées pertinentes, puis à l’ajuster, l’examiner, le tester, et l’améliorer progressivement. Cette approche vise moins à identifier le meilleur modèle qu’à explorer différentes variantes pour mieux comprendre le système étudié.

Pour évaluer la capacité prédictive d’un modèle, on peut s’appuyer sur des données déjà utilisées pour l’ajustement (prédiction interne) ou, de manière plus fiable, sur de nouvelles données (prédiction externe). Cette dernière approche nécessite toutefois de diviser les données en un jeu d’apprentissage et un jeu de test. À défaut, il est possible d’estimer les performances prédictives sur les données d’apprentissage elles-mêmes à l’aide d’outils comme le WAIC ou le LOO-CV.

Le WAIC (Watanabe-Akaike Information Criterion) et le LOO-CV (Leave-One-Out cross-validation) permettent de comparer des modèles en estimant leur capacité à prédire de nouvelles données. Ils combinent l’ajustement aux données observées avec une pénalisation de la complexité du modèle. Une valeur de WAIC ou de LOO-CV plus faible indique un meilleur modèle. Le WAIC est basé sur une approximation théorique, tandis que le LOO-CV repose sur une validation croisée. Le LOO-CV est généralement plus précis, surtout pour les modèles complexes ou les jeux de données de taille limitée, mais il est aussi plus coûteux en calcul. En pratique, lorsque les modèles sont bien spécifiés et que l’échantillon est grand, WAIC et LOO-CV donnent souvent des résultats très proches pour un même modèle.

Je reviens à l’exemple de la régression linéaire. On aimerait tester l’hypothèse que la variable \(x\) explique bien une part importante de la variation dans \(y\). Cela revient à comparer les modèles avec et sans cette variable.

Dans brms, on ajuste ces deux modèles avec des priors faiblement informatifs :

# Modèle avec covariable
fit1 <- brm(y ~ x, data = data, family = gaussian(),
            prior = c(
              prior(normal(0, 1.5), class = Intercept),
              prior(normal(0, 1.5), class = b),
              prior(exponential(1), class = sigma)
            ))

# Modèle sans covariable
fit0 <- brm(y ~ 1, data = data, family = gaussian(),
            prior = c(
              prior(normal(0, 1.5), class = Intercept),
              prior(exponential(1), class = sigma))

La fonction waic() permet d’extraire le WAIC, où le modèle avec la plus petite valeur est préféré. Si le modèle avec \(x\) est bien le bon (c’est ce qu’on attend puisque c’est comme ça que les données ont été simulées), on devrait voir qu’il est nettement meilleur que celui sans covariable :

# Calcul du WAIC pour chaque modèle
waic1 <- waic(fit1)
waic0 <- waic(fit0)

# Comparaison
waic1$estimates['waic',]
#>  Estimate        SE 
#> 172.43145  13.14333
waic0$estimates['waic',]
#>  Estimate        SE 
#> 334.03145  17.13167

Ouf, c’est bien le cas. La fonction loo() permet de calculer le LOO-CV (une approximation en fait) :

# Leave-one-out cross-validation
loo1 <- loo(fit1)
loo0 <- loo(fit0)

# Comparaison
loo_compare(loo0, loo1)
#>      elpd_diff se_diff
#> fit1   0.0       0.0  
#> fit0 -80.8       9.1

Dans cette sortie R, elpd_diff donne l’écart de LOO-CV entre chaque modèle et celui qui a la plus grande valeur. Ainsi, le meilleur modèle est sur la première ligne avec un elpd_diff égal à zéro ; ici, c’est le modèle avec la covariable. On arrive donc à la même conclusion qu’avec le WAIC.

On peut obtenir les valeurs de WAIC avec NIMBLE également. Pour ce faire il suffit d’ajouter WAIC = TRUE dans l’appel à la fonction nimbleMCMC:

# Code du modèle avec covariable
model_avec <- nimbleCode({
  # les priors
  beta0 ~ dnorm(0, sd = 1.5) # prior normal sur l'intercept
  beta1 ~ dnorm(0, sd = 1.5) # prior normal sur le coefficient
  sigma ~ dexp(1) # prior exponentiel sur l'écart-type
  # la vraisemblance
  for(i in 1:n) {
    y[i] ~ dnorm(beta0 + beta1 * x[i], sd = sigma) # equiv de yi = beta0 + beta1 * xi + epsiloni
  }
})

# Code du modèle sans covariable
model_sans <- nimbleCode({
  # les priors
  beta0 ~ dnorm(0, sd = 1.5) # prior normal sur l'intercept
  sigma ~ dexp(1) # prior exponentiel sur l'écart-type
  # la vraisemblance
  for(i in 1:n) {
    y[i] ~ dnorm(beta0, sd = sigma) # equiv de yi = beta0 + beta1 * xi + epsiloni
  }
})

# Données, valeurs initiales
dat <- list(x = x, y = y, n = n) # données
inits_avec <- list(list(beta0 = -0.5, beta1 = -0.5, sigma = 0.1), # valeurs initiales chaine 1
                   list(beta0 = 0, beta1 = 0, sigma = 1), # valeurs initiales chaine 2
                   list(beta0 = 0.5, beta1 = 0.5, sigma = 0.5)) # valeurs initiales chaine 3
inits_sans <- list(list(beta0 = -0.5, sigma = 0.1), # valeurs initiales chaine 1
                   list(beta0 = 0, sigma = 1), # valeurs initiales chaine 2
                   list(beta0 = 0.5, sigma = 0.5)) # valeurs initiales chaine 3

# Modèle avec covariable
lm.avec <- nimbleMCMC(
  code = model_avec,
  data = dat,
  inits = inits_avec,
  niter = 2000,
  nburnin = 1000,
  nchains = 3,
  WAIC = TRUE)
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|

# Modèle sans covariable
lm.sans <- nimbleMCMC(
  code = model_sans,
  data = dat,
  inits = inits_sans,
  niter = 2000,
  nburnin = 1000,
  nchains = 3,
  WAIC = TRUE)
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#> |-------------|-------------|-------------|-------------|
#> |-------------------------------------------------------|
#>   [Warning] There are 1 individual pWAIC values that are greater than 0.4. This may indicate that the WAIC estimate is unstable (Vehtari et al., 2017), at least in cases without grouping of data nodes or multivariate data nodes.

# Calcul du WAIC pour chaque modèle
lm.avec$WAIC$WAIC
#> [1] 172.4424
lm.sans$WAIC$WAIC
#> [1] 333.3443

On arrive à la même conclusion qu’avec brms. A noter que NIMBLE ne fournit pas directement une fonction loo() comme brms, même si on pourrait estimer le LOO-CV à la main.

5.5 En résumé

• La régression linéaire permet de modéliser la relation entre une variable réponse continue et une ou plusieurs variables explicatives, en tenant compte d’une variabilité résiduelle.

• Simuler des données à partir d’un modèle est un excellent moyen de comprendre son fonctionnement et de tester son code.

• Les lois a priori faiblement informatives (comme \(N(0, 1.5)\) pour les coefficients ou \(\text{Exp}(1)\) pour \(\sigma\)) aident à encadrer les valeurs réalistes tout en laissant au modèle la liberté d’apprendre des données.

• La validation et la comparaison des modèles peuvent se faire à l’aide de posterior predictive checks et de critères comme le WAIC. Ces outils permettent d’évaluer la qualité du modèle au regard des données, et d’arbitrer entre plusieurs modèles concurrents.